有一广告气球，直径为6 m，如图所示，放在公司大楼的上空，当行人仰望气球的中心的仰角∠BAC＝30°时，测得气球的视角θ＝2°，若θ的弧度数很小时，可取sinθ＝θ，由此可估计该气球的高BC约为_____________．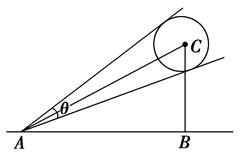
中，
且
（
是正整数)，则数列的通项公式
.
，
的前
项和分别为
，若
，则
_________.
满足
，则公比
__________.
，则
________.
、
、
、9成等差数列，则
____________.推荐套卷
有一广告气球，直径为6 m，如图所示，放在公司大楼的上空，当行人仰望气球的中心的仰角∠BAC＝30°时，测得气球的视角θ＝2°，若θ的弧度数很小时，可取sinθ＝θ，由此可估计该气球的高BC约为_____________．
粤公网安备 44130202000953号