如图,在四棱锥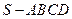 中,底面
中,底面 是正方形,其他四个侧面都是等边三角形,
是正方形,其他四个侧面都是等边三角形,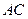 与
与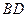 的交点为O.
的交点为O.
(Ⅰ)求证: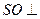 平面
平面 ;
;
(Ⅱ)已知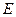 为侧棱
为侧棱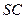 上一个动点. 试问对于
上一个动点. 试问对于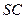 上任意一点
上任意一点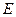 ,平面
,平面 与平面
与平面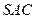 是否垂直?若垂直,请加以证明;若不垂直,请
是否垂直?若垂直,请加以证明;若不垂直,请 说明理由.
说明理由.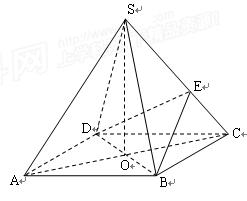
推荐套卷
如图,在四棱锥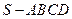 中,底面
中,底面 是正方形,其他四个侧面都是等边三角形,
是正方形,其他四个侧面都是等边三角形,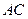 与
与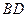 的交点为O.
的交点为O.
(Ⅰ)求证: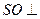 平面
平面 ;
;
(Ⅱ)已知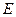 为侧棱
为侧棱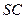 上一个动点. 试问对于
上一个动点. 试问对于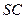 上任意一点
上任意一点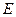 ,平面
,平面 与平面
与平面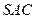 是否垂直?若垂直,请加以证明;若不垂直,请
是否垂直?若垂直,请加以证明;若不垂直,请 说明理由.
说明理由.