已知向量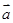
=（
），
=（
,
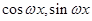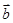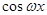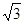
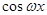），其中（
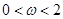）．函数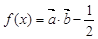
，其图象的一条对称轴为
．
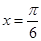（I）求函数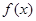
的表达式及单调递增区间；
（Ⅱ）在△ABC中，a、b、c分别为角A、B、C的对边，S为其面积，若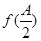
=1，b=l，S△ABC=
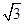，求a的值．
（a为常数）是奇函数.
的定义域；
时，
恒成立．求实数
的取值范围.
.
；
，求实数a.
（Ⅰ）判断
的奇偶性；（Ⅱ）求
（其值用
表示）
是奇函数，且
时
则
推荐套卷
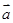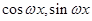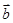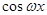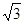
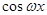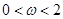已知向量=（），=（,），其中（）．函数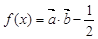，其图象的一条对称轴为．
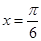（I）求函数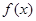的表达式及单调递增区间；
（Ⅱ）在△ABC中，a、b、c分别为角A、B、C的对边，S为其面积，若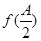=1，b=l，S△ABC=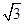，求a的值．
粤公网安备 44130202000953号