(本小题满分14分 )
)
若由数列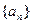 生成的数列
生成的数列 满足对任意的
满足对任意的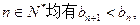 其中
其中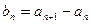 ,则称数列
,则称数列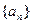 为“Z数列”。
为“Z数列”。
(I)在数列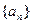 中,已知
中,已知 ,试判断数列
,试判断数列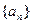 是否为“Z数列”;
是否为“Z数列”;
( II)若数列
II)若数列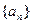 是“Z数列”,
是“Z数列”,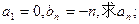
(III)若数列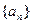 是“Z数列”,设
是“Z数列”,设 求证
求证
推荐套卷
(本小题满分14分 )
)
若由数列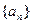 生成的数列
生成的数列 满足对任意的
满足对任意的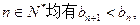 其中
其中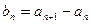 ,则称数列
,则称数列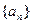 为“Z数列”。
为“Z数列”。
(I)在数列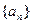 中,已知
中,已知 ,试判断数列
,试判断数列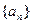 是否为“Z数列”;
是否为“Z数列”;
( II)若数列
II)若数列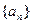 是“Z数列”,
是“Z数列”,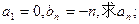
(III)若数列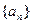 是“Z数列”,设
是“Z数列”,设 求证
求证