如图(1),△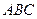 是等腰直角三角形,
是等腰直角三角形,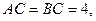 E、F分别为AC、AB的中点,将△AEF沿EF折起,使
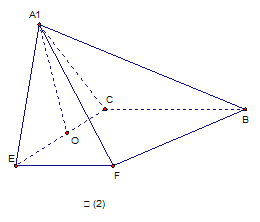
E、F分别为AC、AB的中点,将△AEF沿EF折起,使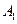 在平面BCEF上的射影O恰好为EC的中点,得到图(2)。
在平面BCEF上的射影O恰好为EC的中点,得到图(2)。
(Ⅰ)求证: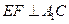 ;(Ⅱ)求三棱锥
;(Ⅱ)求三棱锥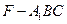 的体积。
的体积。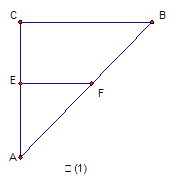
相关知识点
推荐套卷
如图(1),△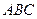 是等腰直角三角形,
是等腰直角三角形,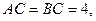 E、F分别为AC、AB的中点,将△AEF沿EF折起,使
E、F分别为AC、AB的中点,将△AEF沿EF折起,使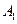 在平面BCEF上的射影O恰好为EC的中点,得到图(2)。
在平面BCEF上的射影O恰好为EC的中点,得到图(2)。
(Ⅰ)求证: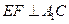 ;(Ⅱ)求三棱锥
;(Ⅱ)求三棱锥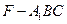 的体积。
的体积。
