(本小题10分) 对定义域分别是 的函数
的函数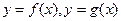 ,
,
规定: 函数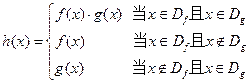
(1) 若函数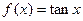 ,
, ,写出函数
,写出函数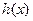 的解析式;
的解析式;
(2) 求问题(1)中函数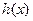 的值域;
的值域;
(3)若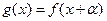 , 其中
, 其中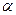 是常数,且
是常数,且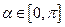 ,请设计一个定义域为R的函数
,请设计一个定义域为R的函数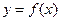 及一个
及一个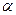 的值,使得
的值,使得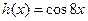 ,并予以证明.
,并予以证明.
推荐套卷
(本小题10分) 对定义域分别是 的函数
的函数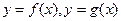 ,
,
规定: 函数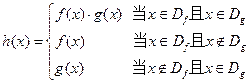
(1) 若函数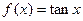 ,
, ,写出函数
,写出函数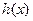 的解析式;
的解析式;
(2) 求问题(1)中函数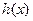 的值域;
的值域;
(3)若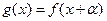 , 其中
, 其中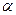 是常数,且
是常数,且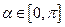 ,请设计一个定义域为R的函数
,请设计一个定义域为R的函数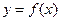 及一个
及一个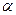 的值,使得
的值,使得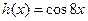 ,并予以证明.
,并予以证明.