(本小题满分12分)
在一次体操选拔赛中,教练组设置了难度不同的甲、乙两个系列,每个系列都有A和B两个动作.比赛时每位运动员自选一个系列完成,两个动作得分之和为该运动员的成绩.
假设每个运动员完成每个系列中的两个动作的得分是相互独立的.根据赛前训练统计数据,某运动员完成甲系列和乙 系列的情况如下表:
系列的情况如下表:
表1:甲系列 表2:乙系列
|
|
现该运动员最后一个出场,之前其他运动员的最高得分为115分.
(Ⅰ)若该运动员希望获得该项目的第一名,应选择哪个系列?说明理由,并求其获得第一名的概率;
(Ⅱ)若该运动员选择乙系列,求其成绩
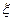 的分布列及其数学期望
的分布列及其数学期望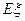 .
.推荐套卷
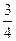
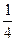
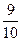
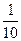
 中,
中,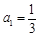 ,且前
,且前 项的算术平均数等于第
项的算术平均数等于第 倍(
倍(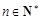 ). (即
). (即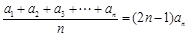
 B ,且C中含有3个元素;(2)
B ,且C中含有3个元素;(2) (
( 表示空集)。
表示空集)。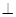 平面ABCD,SD=2a,
平面ABCD,SD=2a, ,点E是SD上的点,且
,点E是SD上的点,且

 ,都有
,都有

 ,直线BE与平面ABCD所成的角为
,直线BE与平面ABCD所成的角为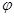 ,若
,若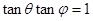 ,求
,求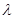 的值
的值 为斜三棱柱
为斜三棱柱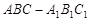 的侧棱
的侧棱 上一点,
上一点,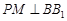 交
交 于点
于点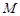 ,
, 交
交 于点
于点 .
.
 ;
; 中有余弦定理:
中有余弦定理: . 拓展到空间,类比三角形的余弦定理,写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式(只写结论,不必证明)
. 拓展到空间,类比三角形的余弦定理,写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式(只写结论,不必证明) 粤公网安备 44130202000953号
粤公网安备 44130202000953号