(本小题满分14分)
已知函数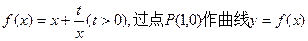 的两条切线PM、PN,切点分
的两条切线PM、PN,切点分 别为M、N.
别为M、N.
(I)当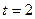 时,求函数
时,求函数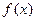 的单调
的单调 递增区间;
递增区间;
(II)设|MN|=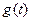 ,试求函数
,试求函数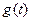 的表达式;
的表达式;
(III)在(II)的条件下,若对任意的正整数 ,在区间
,在区间 内,总存在m+1个数
内,总存在m+1个数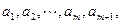 使得不等式
使得不等式 成立,求m的最大值.
成立,求m的最大值.
相关知识点
推荐套卷
(本小题满分14分)
已知函数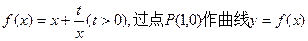 的两条切线PM、PN,切点分
的两条切线PM、PN,切点分 别为M、N.
别为M、N.
(I)当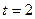 时,求函数
时,求函数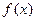 的单调
的单调 递增区间;
递增区间;
(II)设|MN|=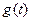 ,试求函数
,试求函数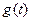 的表达式;
的表达式;
(III)在(II)的条件下,若对任意的正整数 ,在区间
,在区间 内,总存在m+1个数
内,总存在m+1个数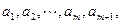 使得不等式
使得不等式 成立,求m的最大值.
成立,求m的最大值.