（本小题满分12分）（注意：在试题卷上作答无效）
已知双曲线
的右顶点为A，右焦点为F，右准线与
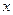轴交于点B，且与一条渐近线交于点C，点O为坐标原点，又
,
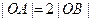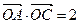过点F的直线与双曲线右支交于点M、N，点P为点M关于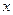轴的对称点。
（Ⅰ）求双曲线的方程；
（Ⅱ）证明：B、P、N三点共线；
，求证：
，且
，求证：
满足
，且有
时，求证：
推荐套卷
（本小题满分12分）（注意：在试题卷上作答无效）
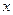已知双曲线的右顶点为A，右焦点为F，右准线与轴交于点B，且与一条渐近线交于点C，点O为坐标原点，又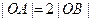,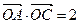过点F的直线与双曲线右支交于点M、N，点P为点M关于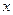轴的对称点。
（Ⅰ）求双曲线的方程；
（Ⅱ）证明：B、P、N三点共线；
粤公网安备 44130202000953号