(本小题满分13分)
某商场为吸引顾客消费推出一项优惠活动.活动规则如下:消费额每满100元可转动如图所示的转盘一次,并获得相应金额的返券,假定指针等可能地停在任一位置.若指针停在A区域返券60元;停在B区域返券30元;停在C区域不返券.例如:消费218元,可转动转盘2次,所获得的返券金额是两次金额之和.
(I)若某位顾客消费128元,求返券金额不低于30元的概率;
(II)若某位顾客恰好消费280元,并按规则 参与了活动,他获得返券的金额记为X(元).
参与了活动,他获得返券的金额记为X(元).
求随机变量X的分布列和数学期望。
相关知识点
推荐套卷
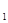 :
: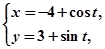 (t为参数), C
(t为参数), C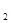 :
: (
(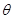 为参数)。
为参数)。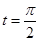 ,Q为C
,Q为C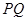 中点
中点 到直线
到直线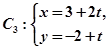 (t为参数)距离的最小值及此时Q点坐标.
(t为参数)距离的最小值及此时Q点坐标. ,其中a,b∈R,e=2.718 28 为自然对数的底数.
,其中a,b∈R,e=2.718 28 为自然对数的底数. 是函数
是函数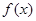 的导函数,求函数g(x)在区间[0,1]上的最小值;
的导函数,求函数g(x)在区间[0,1]上的最小值;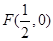 为抛物线
为抛物线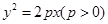 的焦点,点
的焦点,点
 与抛物线交于异于M,N的A,B两点,且
与抛物线交于异于M,N的A,B两点,且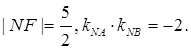
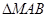 面积最小的直线
面积最小的直线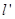 ,若存在,求出直线
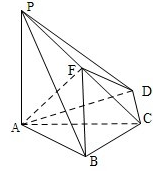
,若存在,求出直线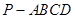 中,
中, .
. ,F为PC的中点,
,F为PC的中点,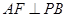 .
.
 的长:
的长: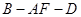 的正弦值.
的正弦值. 、
、 ,设
,设 为坐标原点,点
为坐标原点,点 的坐标为
的坐标为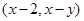 ,记
,记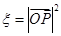 .
. 的最大值,并求事件“
的最大值,并求事件“ 粤公网安备 44130202000953号
粤公网安备 44130202000953号