若一个数列各项取倒数后按原来的顺序构成等差数列,则称这个数列为调和数列.已知数列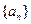 是调和数列,对于各项都是正数的数列
是调和数列,对于各项都是正数的数列 ,满足
,满足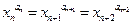
 .
.
(Ⅰ)证明数列 是等比数列;
是等比数列;
(Ⅱ)把数列 中所有项按如图所示的规律排成一个三角形
中所有项按如图所示的规律排成一个三角形
数表,当 时,求第
时,求第 行各数的和;
行各数的和;
(Ⅲ)对于(Ⅱ)中的数列 ,证明:
,证明: .
.
推荐套卷
若一个数列各项取倒数后按原来的顺序构成等差数列,则称这个数列为调和数列.已知数列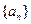 是调和数列,对于各项都是正数的数列
是调和数列,对于各项都是正数的数列 ,满足
,满足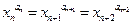
 .
.
(Ⅰ)证明数列 是等比数列;
是等比数列;
(Ⅱ)把数列 中所有项按如图所示的规律排成一个三角形
中所有项按如图所示的规律排成一个三角形
数表,当 时,求第
时,求第 行各数的和;
行各数的和;
(Ⅲ)对于(Ⅱ)中的数列 ,证明:
,证明: .
.