某工厂师徒二人各加工相同型号的零件2个，是否加工出精品均互不影响.已知师父加工一个零件是精品的概率为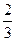
，师徒二人各加工2个零件都是精品的概率为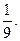
（I）求徒弟加工2个零件都是精品的概率；
（II）求徒弟加工该零件的精品数多于师父的概率；
（III）设师徒二人加工出的4个零件中精品个数为
，求的分布列与均值E.
相关试题
是A，B，C所对的边，S是该三角形的面积，且
。
，
，求
的值。
中，
，
． 
的值；
，求
（ω＞0）
）上是增函数，求ω最大值
的最小正周期、最大值、最小值推荐套卷
某工厂师徒二人各加工相同型号的零件2个，是否加工出精品均互不影响.已知师父加工一个零件是精品的概率为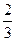，师徒二人各加工2个零件都是精品的概率为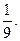
（I）求徒弟加工2个零件都是精品的概率；
（II）求徒弟加工该零件的精品数多于师父的概率；
（III）设师徒二人加工出的4个零件中精品个数为，求的分布列与均值E.
粤公网安备 44130202000953号