如图,两个圆形转盘A,B,每个转盘阴影部分各占转盘面积的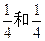 。某“幸运转盘积分活动”规定,当指针指到A,B转盘阴影部分时,分别赢得积分1000分和2000分。先转哪个转盘由参与者选择,若第一次赢得积分,可继续转为另一个转盘,此时活动结束,若第一次未赢得积分,则终止活动。
。某“幸运转盘积分活动”规定,当指针指到A,B转盘阴影部分时,分别赢得积分1000分和2000分。先转哪个转盘由参与者选择,若第一次赢得积分,可继续转为另一个转盘,此时活动结束,若第一次未赢得积分,则终止活动。
(1)记先转A转盘最终所得积分为随机量X,则X的取值分别是多少?
(2)如果你参加此活动,为了赢得更多的积分,你将选择先转哪个转盘?请说明理由。
推荐套卷
如图,两个圆形转盘A,B,每个转盘阴影部分各占转盘面积的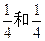 。某“幸运转盘积分活动”规定,当指针指到A,B转盘阴影部分时,分别赢得积分1000分和2000分。先转哪个转盘由参与者选择,若第一次赢得积分,可继续转为另一个转盘,此时活动结束,若第一次未赢得积分,则终止活动。
。某“幸运转盘积分活动”规定,当指针指到A,B转盘阴影部分时,分别赢得积分1000分和2000分。先转哪个转盘由参与者选择,若第一次赢得积分,可继续转为另一个转盘,此时活动结束,若第一次未赢得积分,则终止活动。
(1)记先转A转盘最终所得积分为随机量X,则X的取值分别是多少?
(2)如果你参加此活动,为了赢得更多的积分,你将选择先转哪个转盘?请说明理由。