两对讲机持有者张三、李四,为卡尔货运公司工作,他们对讲机的接收范围是25km,下午3:00张三在基地正东30km内部处,向基地行驶,李四在基地正北40km内部处,向基地行驶,试问下午3:00,他们可以交谈的概率。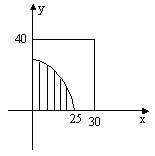
相关知识点
推荐套卷
两对讲机持有者张三、李四,为卡尔货运公司工作,他们对讲机的接收范围是25km,下午3:00张三在基地正东30km内部处,向基地行驶,李四在基地正北40km内部处,向基地行驶,试问下午3:00,他们可以交谈的概率。