(本小题满分12分)有一种密码,明文是由三个字符组成,密码是由明文对应的五个数字组成,编码规则如下表:明文由表中每一排取一个字符组成,且第一排取的字符放在第一位,第二排取的字符放在第二位,第三排取的字符放在第三位,对应的密码由明文对应的数字按相同的次序排成一组组成.
第一排
|
明文字符
|
A
|
B
|
C
|
D
|
密码字符
|
11
|
12
|
13
|
14
|
第二排
|
明文字符
|
E
|
F
|
G
|
H
|
密码字符
|
21
|
22
|
23
|
24
|
第三排
|
明文字符
|
M
|
N
|
P
|
Q
|
密码字符
|
1
|
2
|
3
|
4
|
设随机变量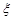 表示密码中所含不同数字的个数.
表示密码中所含不同数字的个数.
(1)求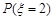 ;
;
(2)求随机变量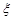 的分布列和它的数学期望.
的分布列和它的数学期望.