右图为一简单组合体,其底面ABCD为正方形, 平面
平面 ,
, ,且
,且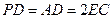 ="2" .
="2" .
(1)答题卡指定的方框内已给出了该几何体的俯视图,请在方框
内画出该几何体的正(主)视图和侧(左)视图;
(2)求四棱锥B-CEPD的体积;
(3)求证: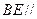 平面
平面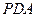 .
.
推荐套卷
右图为一简单组合体,其底面ABCD为正方形, 平面
平面 ,
, ,且
,且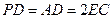 ="2" .
="2" .
(1)答题卡指定的方框内已给出了该几何体的俯视图,请在方框
内画出该几何体的正(主)视图和侧(左)视图;
(2)求四棱锥B-CEPD的体积;
(3)求证: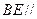 平面
平面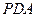 .
.