如图，我市拟在长为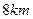
的道路
的一侧修建一条运动赛道。赛道的前一部分为曲线段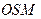
，该曲线段为函数
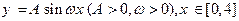的图像，且图像的最高点为
；赛道的后一部分为折线段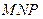
，为保证参赛运动员的安全，限定
。
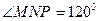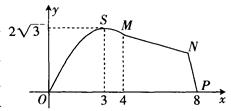
（1）求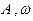
的值和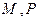
两点间的距离
（2）应如何设计，才能使折线段赛道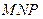最长
相关试题
，(2)tan
·tanβ＝2－
同时成立？若存在，求出锐角α、β的值；若不存在，说明理由．
.
[tan(18°－x)＋tan(12°＋x)]．
，cosα＋cosβ＝
，求cos2
的值．
，化简
＋
.推荐套卷
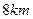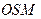如图，我市拟在长为的道路的一侧修建一条运动赛道。赛道的前一部分为曲线段，该曲线段为函数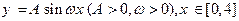的图像，且图像的最高点为；赛道的后一部分为折线段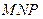，为保证参赛运动员的安全，限定。
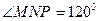（1）求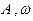的值和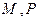两点间的距离
（2）应如何设计，才能使折线段赛道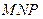最长
粤公网安备 44130202000953号