A.选修4-1 几何证明选讲
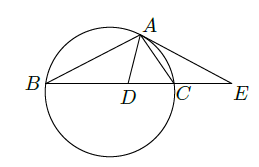
如图,设 的外接圆的切线 与 的延长线交于点 , 的平分线与 交于点 .求证: .
B.选修4-2 矩阵与变换
在平面直角坐标系 中,设椭圆 在矩阵对应的变换作用下得到曲线 ,求 的方程.
C.选修4-4 参数方程与极坐标
在平面直角坐标系 中,点 是椭圆 上的一个动点,求 的最大值.
D.选修4-5 不等式证明选讲
设 为正实数,求证: .
推荐套卷
A.选修4-1 几何证明选讲
如图,设 的外接圆的切线 与 的延长线交于点 , 的平分线与 交于点 .求证: .

B.选修4-2 矩阵与变换
在平面直角坐标系 中,设椭圆 在矩阵对应的变换作用下得到曲线 ,求 的方程.
C.选修4-4 参数方程与极坐标
在平面直角坐标系 中,点 是椭圆 上的一个动点,求 的最大值.
D.选修4-5 不等式证明选讲
设 为正实数,求证: .