已知椭圆
，通径长为1，且焦点与短轴两端点构成等边三角形，（1）求椭圆的方程；（2）过点Q（－1，0）的直线l交椭圆于A，B两点，交直线x=－4于点E，点Q分
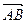所成比为λ，点E分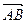所成比为μ，求证λ+μ为定值，并计算出该定值.
相关试题
中，
，
为角分线．
作直线交
于不同两点
，且满足
，求证：
．
的前
项和
（
），数列
的前
（
的前
的前
，
满足
，
，函数
．
化成
的形式；
的值域．
中，角
对边分别为
，且
．
；
，求
中，四边形
是边长为4的正方形，平面
⊥平面
．
⊥平面
是线段
的中点，请问在线段
是否存在点
，使得
面
的大小．推荐套卷
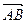已知椭圆，通径长为1，且焦点与短轴两端点构成等边三角形，（1）求椭圆的方程；（2）过点Q（－1，0）的直线l交椭圆于A，B两点，交直线x=－4于点E，点Q分 所成比为λ，点E分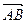所成比为μ，求证λ+μ为定值，并计算出该定值.
粤公网安备 44130202000953号