某公司按现有能力,每月收入为70万元,公司分析部门测算,若不进行改革,入世后因竞争加剧收入将逐月减少.分析测算得入世第一个月收入将减少3万元,以后逐月多减少2万元,如果进行改革,即投入技术改造300万元,且入世后每月再投入1万元进行员工培训,则测算得自入世后第一个月起累计收入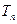 与时间n(以月为单位)的关系为
与时间n(以月为单位)的关系为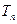 =
= ,且入世第一个月时收入将为90万元,第二个月时累计收入为170万元,问入世后经过几个月,该公司改革后的累计纯收入高于不改革时的累计纯收入.
,且入世第一个月时收入将为90万元,第二个月时累计收入为170万元,问入世后经过几个月,该公司改革后的累计纯收入高于不改革时的累计纯收入.
推荐套卷
某公司按现有能力,每月收入为70万元,公司分析部门测算,若不进行改革,入世后因竞争加剧收入将逐月减少.分析测算得入世第一个月收入将减少3万元,以后逐月多减少2万元,如果进行改革,即投入技术改造300万元,且入世后每月再投入1万元进行员工培训,则测算得自入世后第一个月起累计收入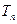 与时间n(以月为单位)的关系为
与时间n(以月为单位)的关系为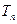 =
= ,且入世第一个月时收入将为90万元,第二个月时累计收入为170万元,问入世后经过几个月,该公司改革后的累计纯收入高于不改革时的累计纯收入.
,且入世第一个月时收入将为90万元,第二个月时累计收入为170万元,问入世后经过几个月,该公司改革后的累计纯收入高于不改革时的累计纯收入.