设 为定义在R上的偶函数,当
为定义在R上的偶函数,当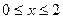 时,
时,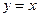 ;当
;当 时,
时, 的图像时顶点在P(3,4),且过点A(2,2)的抛物线的一部分
的图像时顶点在P(3,4),且过点A(2,2)的抛物线的一部分
(1)求函数 在
在 上的解析式;
上的解析式;
(2)在右面的直角坐标系中直接画出函数 的图像;
的图像;
(3)写出函数 值域。
值域。
相关知识点
推荐套卷
设 为定义在R上的偶函数,当
为定义在R上的偶函数,当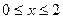 时,
时,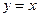 ;当
;当 时,
时, 的图像时顶点在P(3,4),且过点A(2,2)的抛物线的一部分
的图像时顶点在P(3,4),且过点A(2,2)的抛物线的一部分
(1)求函数 在
在 上的解析式;
上的解析式;
(2)在右面的直角坐标系中直接画出函数 的图像;
的图像;
(3)写出函数 值域。
值域。