(本小题满分12分)
湖南省有许多旅游景点，某同学利用寒暑假旅游了张家界、南岳、韶山、岳阳楼和桃花源等5个景点，并收藏有张家界纪念门票3张，南岳纪念门票2张，韶山、岳阳楼、桃花源纪念门票各1张，现从中随机抽取5张.
（Ⅰ）求抽取的5张门票中恰有3个或恰有4个景点的概率；
（Ⅱ）若抽取的5张门票中5个景点都有记10分，恰有4个景点记8分，恰有3个景点记6分，依此类推.设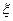
表示所得的分数，求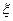的分布列和数学期望.
相关试题
的不等式
的解集是空集，求实数
的取值范围
都是正数．
，求
的最大值；
，求
的最小值．
．
的单调递增区间；
的方程
在
]上有两个不同的解，求实数
的取值范围．
的各项均为正数，且
，
，求数列
的前
项和．推荐套卷
(本小题满分12分)
湖南省有许多旅游景点，某同学利用寒暑假旅游了张家界、南岳、韶山、岳阳楼和桃花源等5个景点，并收藏有张家界纪念门票3张，南岳纪念门票2张，韶山、岳阳楼、桃花源纪念门票各1张，现从中随机抽取5张.
（Ⅰ）求抽取的5张门票中恰有3个或恰有4个景点的概率；
（Ⅱ）若抽取的5张门票中5个景点都有记10分，恰有4个景点记8分，恰有3个景点记6分，依此类推.设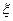表示所得的分数，求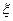的分布列和数学期望.
粤公网安备 44130202000953号