购买某种保险，每个投保人每年度向保险公司交纳保费
元，若投保人在购买保险的一年度内出险，则可以获得10000元的赔偿金．假定在一年度内有10000人购买了这种保险，且各投保人是否出险相互独立．已知保险公司在一年度内至少支付赔偿金10000元的概率为
.
（Ⅰ）求一投保人在一年度内出险的概率
.
（Ⅱ）设保险公司开办该项险种业务除赔偿金外的成本为50000元，为保证盈利的期望不小于0，求每位投保人应交纳的最低保费（单位：元）.
相关试题
在椭圆
上，求点
的最大距离和最小距离。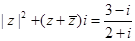
，其中
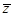是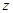
的共轭复数，求复数
.
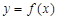在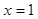
处的切线的方程为
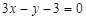，求实数a的值；
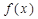≥0恒成立的充要条件是
；
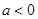，且对任意
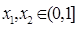，都有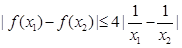
，求实数a的取值范围.统计表明，某种型号的汽车在匀速行驶中每小时耗油量y（升）关于行驶速度x（千米/小时）的函数解析式可以表示为：
(
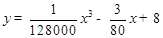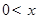≤120).已知甲、乙两地相距100千米.
（Ⅰ）当汽车以40千米/小时的速度匀速行驶时，从甲地到乙地要耗油多少升？
（Ⅱ）当汽车以多大的速度匀速行驶时，从甲地到乙地耗油最少？最少为多少升？
中，底面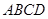
为平行四边形，
，
，
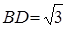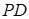⊥底面
平面
； 
为
，求
与平面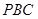
所成角的正弦值.
相关知识点
推荐套卷
粤公网安备 44130202000953号