在五棱锥P-ABCDE中,PA=AB=AE=4a,PB=PE= a,BC=DE=2a,∠EAB=∠ABC=∠DEA=90°.(1)若
a,BC=DE=2a,∠EAB=∠ABC=∠DEA=90°.(1)若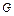 为
为 中点,求证:
中点,求证: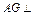 平面
平面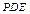 .
.
(2)求二面角A-PD-E的正弦值;(3)求点C到平面PDE的距离.
推荐套卷
在五棱锥P-ABCDE中,PA=AB=AE=4a,PB=PE= a,BC=DE=2a,∠EAB=∠ABC=∠DEA=90°.(1)若
a,BC=DE=2a,∠EAB=∠ABC=∠DEA=90°.(1)若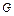 为
为 中点,求证:
中点,求证: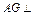 平面
平面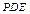 .
.
(2)求二面角A-PD-E的正弦值;(3)求点C到平面PDE的距离.