袋中装有大小相同的2个白球和3个黑球．
（Ⅰ）采取放回抽样方式，从中依次摸出两个球，求两球颜色不同的概率；
（Ⅱ）采取不放回抽样方式，从中依次摸出两个球，记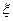
为摸出两球中白球的个数，求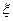的期望和方差.
相关试题
，已知
，
的值；
，求
的值
的解集为
和
的值； (2)求不等式
的解集
的不等式
的解集是（－1，3），求实数 
的值。
的不等式
相关知识点
推荐套卷
袋中装有大小相同的2个白球和3个黑球．
（Ⅰ）采取放回抽样方式，从中依次摸出两个球，求两球颜色不同的概率；
（Ⅱ）采取不放回抽样方式，从中依次摸出两个球，记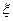为摸出两球中白球的个数，求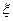的期望和方差.
粤公网安备 44130202000953号