设函数f（x）＝a·b，其中向量a＝（cos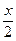
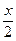，sin），（x∈R），向量b＝（cosj，sinj)
（Ⅰ）求j的值；
（Ⅱ）若函数y＝1＋sin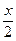的图象按向量c＝（m，n）（| m |＜p)平移可得到函数
y＝f（x）的图象，求向量c．
相关试题
γ=a
求证：a⊥α
平面ABC，PA=PB=PC，∠APB=∠APC=60°，∠BPC=90°求证：平面ABC⊥平面PBC
推荐套卷
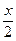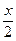设函数f（x）＝a·b，其中向量a＝（cos，sin），（x∈R），向量b＝（cosj，sinj)
（Ⅰ）求j的值；
（Ⅱ）若函数y＝1＋sin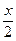的图象按向量c＝（m，n）（| m |＜p)平移可得到函数
y＝f（x）的图象，求向量c．
粤公网安备 44130202000953号