（本小题满分12分）一束光线从点
出发，经直线l:
上一点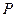
反射后，恰好穿过点
．（1）求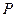点的坐标；（2）求以
、
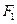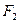为焦点且过点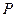的椭圆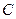
的方程； （3）设点
是椭圆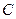上除长轴两端点外的任意一点，试问在
轴上是否存在两定点
、
，使得直线
、
的斜率之积为定值？若存在，请求出定值，并求出所有满足条件的定点、的坐标；若不存在，请说明理由．
相关试题
，
．若
是
的必要不充分条件，求实数
的取值范围 ．
，
；命题
关于
的方程
有两个小于1的正根 ．试分析
是
的什么条件 ．
，则
”的形式，并写出它的逆命题、否命题与逆否命题，并分别判断其真假 ．推荐套卷
（本小题满分12分）一束光线从点出发，经直线l:上一点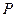反射后，恰好穿过点．（1）求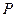点的坐标；（2）求以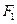、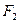为焦点且过点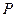的椭圆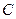的方程； （3）设点是椭圆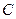上除长轴两端点外的任意一点，试问在轴上是否存在两定点、，使得直线、的斜率之积为定值？若存在，请求出定值，并求出所有满足条件的定点、的坐标；若不存在，请说明理由．
粤公网安备 44130202000953号