已知函数 ,
, 、
、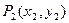 是
是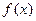 图像上两点.
图像上两点.
(1)若 ,求证:
,求证: 为定值;
为定值;
(2)设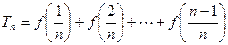 ,其中
,其中 且
且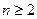 ,求
,求 关于
关于 的解析式;
的解析式;
(3)对(2)中的 ,设数列
,设数列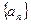 满足
满足 ,当
,当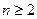 时,
时, ,问是否存在角
,问是否存在角 ,使不等式
,使不等式 …
…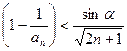 对一切
对一切 都成立?若存在,求出角
都成立?若存在,求出角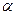 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
推荐套卷
已知函数 ,
, 、
、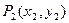 是
是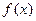 图像上两点.
图像上两点.
(1)若 ,求证:
,求证: 为定值;
为定值;
(2)设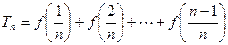 ,其中
,其中 且
且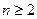 ,求
,求 关于
关于 的解析式;
的解析式;
(3)对(2)中的 ,设数列
,设数列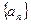 满足
满足 ,当
,当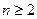 时,
时, ,问是否存在角
,问是否存在角 ,使不等式
,使不等式 …
…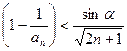 对一切
对一切 都成立?若存在,求出角
都成立?若存在,求出角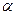 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.