如图所示，在直角梯形ABCP中，AB=BC=3，AP=7，CD⊥AP，现将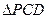
沿折线CD折成60°的二面角P—CD—A，设E，F，G分别是PD，PC，BC的中点。
（I）求证：PA//平面EFG；
（II）若M为线段CD上的一个动点，问当M在什么位置时，MF与平面EFG所成角最大。
相关试题
满足条件：
；②函数
的图像与直线
相切．
在
时恒成立，求实数
的取值范围．
的直线与曲线
和
都相切，求
的值.
.
的奇偶性；(3)求证:
的中心在坐标原点，焦点在
轴上，椭圆
，最小值为
．
与椭圆交于不同的两点
、
，且线段
的垂直平分线过定点
，求
的取值范围。推荐套卷
如图所示，在直角梯形ABCP中，AB=BC=3，AP=7，CD⊥AP，现将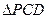沿折线CD折成60°的二面角P—CD—A，设E，F，G分别是PD，PC，BC的中点。
（I）求证：PA//平面EFG；
（II）若M为线段CD上的一个动点，问当M在什么位置时，MF与平面EFG所成角最大。
粤公网安备 44130202000953号