已知长方形ABCD, AB=2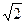
, BC="1." 以AB的中点
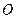为原点建立如图8所示的平面直角坐标系
.
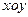(Ⅰ)求以A、B为焦点，且过C、D两点的椭圆的标准方程;
(Ⅱ)过点P(0,2)的直线
交(Ⅰ)中椭圆于M,N两点,是否存在直线,使得以弦MN为直径的圆恰好过原点?若存在,求出直线的方程;若不存在,说明理由.
相关试题
，函数
的定义域为
，
．
．
的左焦点
为圆
的圆心，且椭圆上的点到点
．
与椭圆交于不同的两点
，点
，求
的值．
中,角
，所对的边分别是
，且
．
的值；
，求
面积的最大值．
的各项均为正数，
是数列
．
的通项公式；
的值．
．
的解集
．求
的值；
．求
的最小值．推荐套卷
已知长方形ABCD, AB=2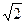, BC="1." 以AB的中点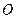为原点建立如图8所示的平面直角坐标系.
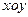(Ⅰ)求以A、B为焦点，且过C、D两点的椭圆的标准方程;
(Ⅱ)过点P(0,2)的直线交(Ⅰ)中椭圆于M,N两点,是否存在直线,使得以弦MN为直径的圆恰好过原点?若存在,求出直线的方程;若不存在,说明理由.
粤公网安备 44130202000953号