（本小题满分13分）某商场准备在暑假期间举行促销活动，根据市场调查，该商场决定从3种服装商品、2种家电商品、4种日用商品中，选出3种商品进行促销活动．（Ⅰ）试求选出的3种商品至少有一种日用商品的概率；（Ⅱ）商场对选出的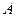
商品采用的促销方案是有奖销售，即在该商品现价的基础上将价格提高180元，同时允许顾客有3次抽奖的机会，若中奖，则每次中奖都可获得一定数额的奖金．假设顾客每次抽奖时获奖与否是等概率的．请问：商场应将中奖奖金数额最高定为多少元，才能使促销方案对自己有利?
相关试题
从参加环保知识竞赛的学生中抽出60名,将其成绩整理后画出的频率分布直方图如下．观察图形，回答下列问题：
（1）49．5——69．5这一组的频率和频数分别为多少?
（2）估计这次环保知识竞赛成绩的中位数及平均成绩．（精确到小数点后一位）
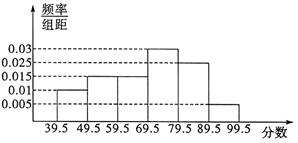
的取值范围为[0,10]，给出如图所示程序框图，输入一个数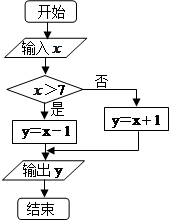
（
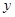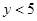）的概率；（3）求输出的
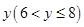的概率．海关对同时从
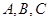三个不同地区进口的某种商品进行抽样检测，从各地区进口此种商品的数量（单位：件）如下表所示，工作人员用分层抽样的方法从这些商品中共抽取6件进行检测．
| 地区 |
 |
 |
 |
| 数量 |
50 |
150 |
100 |
（1）求这6件样品中来自各地区商品的数量；
（2）若在这6件样品中随机抽取2件送往甲机构进一步检测，求这2件商品来自相同地区的概率．
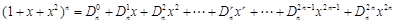的展开式中，把
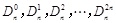叫做三项式系数．
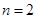时，写出三项式系数
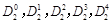的值；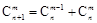
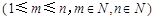，给出一个关于三项式系数
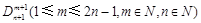的相似性质，并予以证明；
的值．
；
．相关知识点
推荐套卷
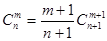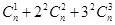
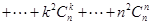粤公网安备 44130202000953号