（本小题满分13分）
某市十所重点中学进行高三联考，共有5000名考生，为了了解数学学科的学习情况，
现从中随机抽出若干名学生在这次测试中的数学成绩，制成如下频率分布表：
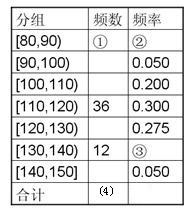
（1）根据上面频率分布表，求①，②，③，④处的数值
（2）在所给的坐标系中画出区间[80，150]上的频率分布直方图；
(3)从整体中任意抽取3个个体,成绩落在［105，120］中的个体数目为ξ ,求ξ的分布列和数
学期望.
相关试题
(其中
且
,
为实常数)．
，求
的值(用
且
对于
恒成立，求实数m的取值范围(用
且
，求函数
的取值范围．
的定义域；
，求
的最大值与最小值。
，求满足
的实数
的取值范围
时，求△ABC的面积的取值范围。推荐套卷
（本小题满分13分）
某市十所重点中学进行高三联考，共有5000名考生，为了了解数学学科的学习情况，
现从中随机抽出若干名学生在这次测试中的数学成绩，制成如下频率分布表：
（1）根据上面频率分布表，求①，②，③，④处的数值
（2）在所给的坐标系中画出区间[80，150]上的频率分布直方图；
(3)从整体中任意抽取3个个体,成绩落在［105，120］中的个体数目为ξ ,求ξ的分布列和数
学期望.
粤公网安备 44130202000953号