已知函数f(x)＝ax3＋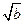
x2－a2x(a＞0),存在实数x1、x2满足下列条件:①x1＜x2;②f¢(x1)＝f¢(x2)＝0;③|x1|＋|x2|＝2.
（I） 证明:0＜a£3；
（II） 求b的取值范围;
（III）若函数h(x)＝f¢(x)－6a(x－x1),证明:当x1＜x＜2时,|h(x)|£12a.
推荐套卷
已知函数f(x)＝ax3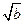＋x2－a2x(a＞0),存在实数x1、x2满足下列条件:①x1＜x2;②f¢(x1)＝f¢(x2)＝0;③|x1|＋|x2|＝2.
（I） 证明:0＜a£3；
（II） 求b的取值范围;
（III）若函数h(x)＝f¢(x)－6a(x－x1),证明:当x1＜x＜2时,|h(x)|£12a.
粤公网安备 44130202000953号