如图，四棱锥P—ABCD的底面ABCD是正方形，侧棱PD⊥底面ABCD，PD=DC，E是PC的中点.
（1）证明PA//平面BDE；
（2）求二面角B—DE—C的平面角的余弦值；
（3）在棱PB上是否存在点F，使PB⊥平面DEF？证明你的结论.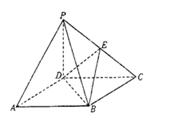 
相关试题
，已知
是奇函数．
求b、c的值；
求
的单调区间与极值．
，
．
，求角
；
，求
的值．
的值．
的首项
．
对任意实数x都满足
，且
．令
.
，证明：对任意
，恒有
．推荐套卷
如图，四棱锥P—ABCD的底面ABCD是正方形，侧棱PD⊥底面ABCD，PD=DC，E是PC的中点.
（1）证明PA//平面BDE；
（2）求二面角B—DE—C的平面角的余弦值；
（3）在棱PB上是否存在点F，使PB⊥平面DEF？证明你的结论.
粤公网安备 44130202000953号