(本小题12分)
设椭圆 右焦点为
右焦点为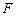 ,它与直线
,它与直线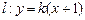 相交于
相交于 、
、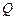 两点,
两点,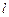 与
与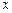 轴的交点
轴的交点 到椭圆左准线的距离为
到椭圆左准线的距离为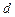 ,若椭圆的焦距
,若椭圆的焦距 是
是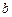 与
与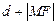 的等差中项.
的等差中项.
⑴求椭圆离心率 ;
;
⑵设点 与点
与点 关于原点
关于原点 对称,若以
对称,若以 为圆心,
为圆心,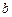 为半径的圆与
为半径的圆与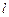 相切,且
相切,且 求椭圆
求椭圆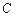 的方程.
的方程.
推荐套卷
(本小题12分)
设椭圆 右焦点为
右焦点为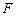 ,它与直线
,它与直线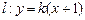 相交于
相交于 、
、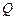 两点,
两点,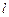 与
与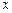 轴的交点
轴的交点 到椭圆左准线的距离为
到椭圆左准线的距离为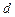 ,若椭圆的焦距
,若椭圆的焦距 是
是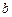 与
与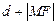 的等差中项.
的等差中项.
⑴求椭圆离心率 ;
;
⑵设点 与点
与点 关于原点
关于原点 对称,若以
对称,若以 为圆心,
为圆心,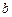 为半径的圆与
为半径的圆与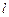 相切,且
相切,且 求椭圆
求椭圆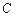 的方程.
的方程.