如图，已知AB⊥平面ACD，DE//AB，△ACD是正三角形，AD=DE=2AB，且F
是CD的中点。
（I）求证：AF//平面BCE；
（II）求证：平面BCE⊥平面CDE；
（III）求平面BCE与平面ACD所成锐二面角的大小。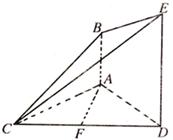
满足
，且
对一切实数
恒成立.
求
；
求
求证：
是二次函数，若
，求
，求
求
，求函数
的解析式
在
上是增函数？若存在求出a的值，若不存在，说明理由。
，
的单调区间和值域；
，函数
，若对于任意
，总存在
使得
成立，求
的取值范围。推荐套卷
如图，已知AB⊥平面ACD，DE//AB，△ACD是正三角形，AD=DE=2AB，且F
是CD的中点。
（I）求证：AF//平面BCE；
（II）求证：平面BCE⊥平面CDE；
（III）求平面BCE与平面ACD所成锐二面角的大小。
粤公网安备 44130202000953号