已知函数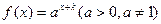
的图象过（－1，1）点，其反函数
的图象过（8，2）点。
（1）求a，k的值；
（2）若将的图象向在平移两个单位，再向上平移1个单位，就得到函数
的图象，写出的解析式；
（3）若函数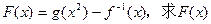
的最小值及取最小值时x的值。
相关试题
.
＋f(x)＝0.
, x∈[3, 5]
｝，B={x|
}，求
，
。
，求a；
满足条件
，及
.
上的最大和最小值.推荐套卷
已知函数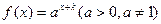的图象过（－1，1）点，其反函数的图象过（8，2）点。
（1）求a，k的值；
（2）若将的图象向在平移两个单位，再向上平移1个单位，就得到函数的图象，写出的解析式；
（3）若函数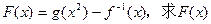的最小值及取最小值时x的值。
粤公网安备 44130202000953号