已知函数
的图象过原点，
，
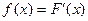，函数y=f(x)与y=g(x)的图象交于不同两点A、B。
（1）若y=F(x)在x=-1处取得极大值2，求函数y=F(x)的单调区间；
（2）若使g(x)=0的x值满足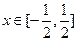
，求线段AB在x轴上的射影长的取值范围；
相关试题
,和命题
,且
为真，
的取值范围．
，
，其中a，b为非零实常数。
的图像得到函数
的图像？
，
，求
的值。
，讨论
的奇偶性（只写结论，不用证明）。
.函数
。
的对称轴。
时,求
的最大值及对应的
值。
夹角是120°.
的值， 
的值；
的值.推荐套卷
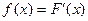已知函数的图象过原点，，，函数y=f(x)与y=g(x)的图象交于不同两点A、B。
（1）若y=F(x)在x=-1处取得极大值2，求函数y=F(x)的单调区间；
（2）若使g(x)=0的x值满足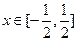，求线段AB在x轴上的射影长的取值范围；
粤公网安备 44130202000953号