过抛物线L：
的焦点F的直线l交此抛物线于A、B两点，
①求
；
②记坐标原点为O，求△OAB的重心G的轨迹方程.
③点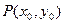
为抛物线L上一定点，M、N为抛物线上两个动点，且满足
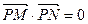，当点M、N在抛物线上运动时，证明直线MN过定点。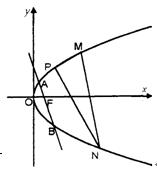
，求
.
．
的最小正周期、最小值、最大值；
区间
内的图象．
，且
与
夹角为
。求：
；（2）
的夹角。
．
,求以
为切点的曲线的切线方程；
恒成立，确定实数K的取值范围；
．相关知识点
推荐套卷
过抛物线L：的焦点F的直线l交此抛物线于A、B两点，
①求；
②记坐标原点为O，求△OAB的重心G的轨迹方程.
③点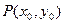为抛物线L上一定点，M、N为抛物线上两个动点，且满足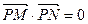，当点M、N在抛物线上运动时，证明直线MN过定点。
粤公网安备 44130202000953号