设不等式组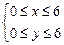
表示的区域为A，不等式组
表示的区域为B，在区域A中任意取一点P
．
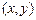（Ⅰ）求点P落在区域B中的概率；
（Ⅱ）若
分别表示甲、乙两人各掷一次正方体骰子所得的点数，求点P落在区域B中的概率．
均为正数，证明：
，
，且
,求证：
.
能够被6整除.相关知识点
推荐套卷
设不等式组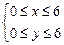表示的区域为A，不等式组表示的区域为B，在区域A中任意取一点P．
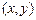（Ⅰ）求点P落在区域B中的概率；
（Ⅱ）若分别表示甲、乙两人各掷一次正方体骰子所得的点数，求点P落在区域B中的概率．
粤公网安备 44130202000953号