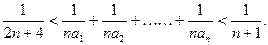设函数f(x)=x2+(lga+2)x+lgb，g(x)=2x+2，若f(－1)=0，且对一切实数x，不等式f(x)≥g(x)恒成立；
（Ⅰ）（本问5分）求实数a、b的值；
（Ⅱ）（本问7分）设F(x)=f(x)－g(x)，数列{an}满足关系an=F(n)，
证明：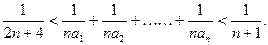
上有一点
,它到焦点的距离等于
,求实数
与
的值.
的抛物线的标准方程.
的解集为
,求不等式
的解集.推荐套卷
设函数f(x)=x2+(lga+2)x+lgb，g(x)=2x+2，若f(－1)=0，且对一切实数x，不等式f(x)≥g(x)恒成立；
（Ⅰ）（本问5分）求实数a、b的值；
（Ⅱ）（本问7分）设F(x)=f(x)－g(x)，数列{an}满足关系an=F(n)，
证明：
粤公网安备 44130202000953号