将圆x2 + y2 + 2x – 2y = 0按向量a= (1,–1)平移得到圆O,直线l和圆O相交于A、B两点,若在圆O上存在点C,使 ,且
,且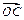 =
= a.
a.
(1)求 的值;(2)求弦AB的长;(3)求直线l的方程.
的值;(2)求弦AB的长;(3)求直线l的方程.
相关知识点
推荐套卷
将圆x2 + y2 + 2x – 2y = 0按向量a= (1,–1)平移得到圆O,直线l和圆O相交于A、B两点,若在圆O上存在点C,使 ,且
,且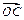 =
= a.
a.
(1)求 的值;(2)求弦AB的长;(3)求直线l的方程.
的值;(2)求弦AB的长;(3)求直线l的方程.