甲，乙两个同学同时报名参加某重点高校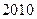
年自主招生，高考前自主招生的程序为审核材料和文化测试，只有审核过关后才能参加文化测试，文化测试合格者即可获得自主招生入选资格.已知甲，乙两人审核过关的概率分别为
，
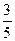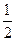，审核过关后，甲，乙两人文化测试合格的概率分别为
，
.
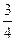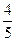(1) 求甲获得自主招生入选资格的概率；
(2) 求甲，乙两人至少有一人通过审核的概率
相关试题
有两个相等的实根。（1）求函数
的解析式；
的奇偶性，并证明。
的定义域。
≤0}， B={x|x2－3x+2<0}， U=R，求（
uA）∩ B．
．
满足
，
（
，
），
是等比数列.
的通项公式；
为奇数时，
；
（相关知识点
推荐套卷
甲，乙两个同学同时报名参加某重点高校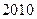年自主招生，高考前自主招生的程序为审核材料和文化测试，只有审核过关后才能参加文化测试，文化测试合格者即可获得自主招生入选资格.已知甲，乙两人审核过关的概率分别为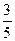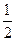，，审核过关后，甲，乙两人文化测试合格的概率分别为，.
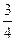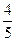(1) 求甲获得自主招生入选资格的概率；
(2) 求甲，乙两人至少有一人通过审核的概率
粤公网安备 44130202000953号