已知函数f (x) = x3 -(l-3)x2 -(l +3)x + l-1(l > 0)在区间[n, m]上为减函数,记m的最大值为m0,n的最小值为n0,且满足m0-n0 = 4.
 (1)求m0,n0的值以及函数f (x)的解析式;
(1)求m0,n0的值以及函数f (x)的解析式;
(2)已知等差数列{xn}的首项 .又过点A(0, f (0)),B(1, f (1))的直线方程为y=g(x).试问:在数列{xn}中,哪些项满足f (xn)>g(xn)?
.又过点A(0, f (0)),B(1, f (1))的直线方程为y=g(x).试问:在数列{xn}中,哪些项满足f (xn)>g(xn)?
(3)若对任意x1,x2∈[a, m0](x1≠x2),都有 成立,求a的最小值.
成立,求a的最小值.
相关知识点
推荐套卷
 设函数
设函数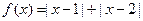
 的解集;
的解集;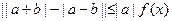 (
( ,
,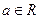 ,
, )恒成立,求实数
)恒成立,求实数 的范围.
的范围. 的参数方程为
的参数方程为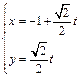 (
(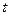 为参数),曲线C的极坐标方程是
为参数),曲线C的极坐标方程是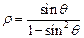 ,以极
,以极 点为原点,极轴为
点为原点,极轴为 轴正方向建立直角坐标系,点
轴正方向建立直角坐标系,点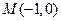 ,直线
,直线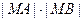 的值.
的值. 于点A,割线PBC经过圆心O,OB=PB=1,OA绕点O逆时针旋转
于点A,割线PBC经过圆心O,OB=PB=1,OA绕点O逆时针旋转 到O D.
到O D.
 的线段?若有,指出该线段;若没有,说明理由.
的线段?若有,指出该线段;若没有,说明理由. 和“伪二次函数”
和“伪二次函数”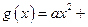
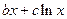 (
(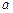 、
、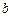 、
、
 ),
), ,无论
,无论 在定义域内不可能总为增函数;
在定义域内不可能总为增函数; ,线段
,线段 中点的横坐标为
中点的横坐标为 ,记直线
,记直线 ,
,  i)求证:
i)求证: ;
; ,是否有(i)同样的性质?证明你的结论.
,是否有(i)同样的性质?证明你的结论.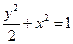 ,斜率为
,斜率为 的直线
的直线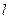 过椭圆的上焦点且与椭圆相交于
过椭圆的上焦点且与椭圆相交于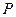 ,
, 两点,线段
两点,线段 的垂直平分线与
的垂直平分线与 轴相交于点
轴相交于点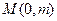 .
. 的取值范围;
的取值范围; 面积的最大值.
面积的最大值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号