点P(x0,y0)在椭圆 1(a>b>0)上,x0=
1(a>b>0)上,x0=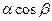 , y0=
, y0=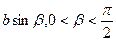 . 直线
. 直线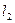 与直线
与直线 :
: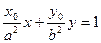 垂直,O为坐标原点,直线OP的倾斜角为
垂直,O为坐标原点,直线OP的倾斜角为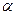 ,直线
,直线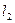 的倾斜角为
的倾斜角为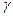 .
.
(Ⅰ)证明:点P是椭圆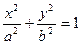 与直线
与直线 的唯一交点;
的唯一交点;
(Ⅱ)证明:tan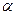 ,tan
,tan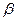 ,tan
,tan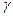 构成等比数列。
构成等比数列。
推荐套卷
点P(x0,y0)在椭圆 1(a>b>0)上,x0=
1(a>b>0)上,x0=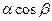 , y0=
, y0=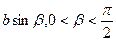 . 直线
. 直线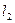 与直线
与直线 :
: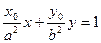 垂直,O为坐标原点,直线OP的倾斜角为
垂直,O为坐标原点,直线OP的倾斜角为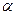 ,直线
,直线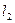 的倾斜角为
的倾斜角为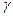 .
.
(Ⅰ)证明:点P是椭圆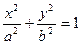 与直线
与直线 的唯一交点;
的唯一交点;
(Ⅱ)证明:tan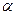 ,tan
,tan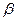 ,tan
,tan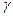 构成等比数列。
构成等比数列。