已知数列{bn}是等差数列,b1=1,b1+b2+…+b10=145.
(1)求数列{bn}的通项公式bn;
(2)设数列{an}的通项an=loga(1+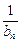 )(其中a>0且a≠1)记Sn是数列{an}的前n项和,试比较Sn与
)(其中a>0且a≠1)记Sn是数列{an}的前n项和,试比较Sn与 logabn+1的大小,并证明你的结论
logabn+1的大小,并证明你的结论
相关知识点
推荐套卷
已知数列{bn}是等差数列,b1=1,b1+b2+…+b10=145.
(1)求数列{bn}的通项公式bn;
(2)设数列{an}的通项an=loga(1+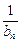 )(其中a>0且a≠1)记Sn是数列{an}的前n项和,试比较Sn与
)(其中a>0且a≠1)记Sn是数列{an}的前n项和,试比较Sn与 logabn+1的大小,并证明你的结论
logabn+1的大小,并证明你的结论