已知M、N两点的坐标分别是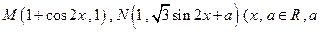 是常数
是常数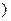 ,令
,令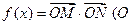 是坐标原点
是坐标原点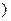 .
.
(Ⅰ)求函数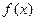 的解析式,并求函数
的解析式,并求函数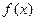 在
在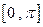 上的单调递增区间;
上的单调递增区间;
(Ⅱ)当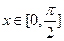 时,
时,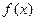 的最大值为
的最大值为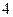 ,求a的值,并说明此时
,求a的值,并说明此时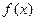 的图象可由函数
的图象可由函数 的图象经过怎样的平移和伸缩变换而得到?
的图象经过怎样的平移和伸缩变换而得到?
推荐套卷
已知M、N两点的坐标分别是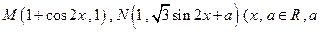 是常数
是常数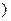 ,令
,令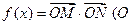 是坐标原点
是坐标原点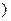 .
.
(Ⅰ)求函数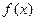 的解析式,并求函数
的解析式,并求函数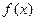 在
在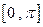 上的单调递增区间;
上的单调递增区间;
(Ⅱ)当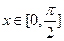 时,
时,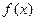 的最大值为
的最大值为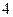 ,求a的值,并说明此时
,求a的值,并说明此时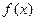 的图象可由函数
的图象可由函数 的图象经过怎样的平移和伸缩变换而得到?
的图象经过怎样的平移和伸缩变换而得到?