已知矩形ABCD的边长AB＝6cm，BC＝4cm，在CD上截取CE＝4cm，以BE为棱将矩形折起，使△BC′E的高C′F⊥平面ABED，求：
（1）点C′到平面ABED的距离；
（2）C′到边AB的距离；
（3）C′到AD的距离．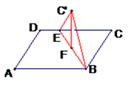
相关知识点
推荐套卷
已知矩形ABCD的边长AB＝6cm，BC＝4cm，在CD上截取CE＝4cm，以BE为棱将矩形折起，使△BC′E的高C′F⊥平面ABED，求：
（1）点C′到平面ABED的距离；
（2）C′到边AB的距离；
（3）C′到AD的距离．
粤公网安备 44130202000953号