已知函数
满足下列条件：对任意的实数x1，x2都有
λ
和
，其中λ是大于0的
常数.实数a0，a，b满足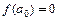 
和b=a-λf（a）.
(Ⅰ)证明:λ≤1，并且不存在
，使得
；
(Ⅱ)证明: (b-a0)2≤(1-λ2)(a-a0)2；
(Ⅲ)证明: [f(b)]2≤(1-λ2)[f(a)]2.
推荐套卷
已知函数满足下列条件：对任意的实数x1，x2都有
λ和，其中λ是大于0的
常数.实数a0，a，b满足 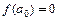和b=a-λf（a）.
(Ⅰ)证明:λ≤1，并且不存在，使得；
(Ⅱ)证明: (b-a0)2≤(1-λ2)(a-a0)2；
(Ⅲ)证明: [f(b)]2≤(1-λ2)[f(a)]2.
粤公网安备 44130202000953号