(本小题满分14分)根据如图所示的程序框图,将输出a,b的值依次分别记为a1,a2, ,an, ,a2008;b1,b2, ,bn, ,b2008.
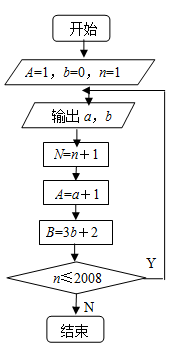
(Ⅰ)求数列 { an } 的通项公式;
(Ⅱ)写出b1,b2,b3,b4,由此猜想{ bn }的通项公式,并证明你的证明;
(Ⅲ)在 ak 与 ak+1 中插入bk+1个3得到一个新数列 { cn } ,设数列 { cn }的前n项和为Sn,问是否存在这样的正整数m,使数列{ cn }的前m项的和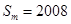 ,如果存在,求出m的值,如果不存在,请说明理由.
,如果存在,求出m的值,如果不存在,请说明理由.